Dynamic PageRank
We propose a dynamical system that captures changes to the network centrality of nodes as external interest in those nodes vary. We derive this system by adding timedependent teleportation to the PageRank score. The result is not a single set of importance scores, but rather a time-dependent set. These can be converted into ranked lists in a variety of ways, for instance, by taking the largest change in the importance score. For an interesting class of the dynamic teleportation functions, we derive closed form solutions for the dynamic PageRank vector. The magnitude of the deviation from a static PageRank vector is given by a PageRank problem with complex-valued teleportation parameters. Moreover, these dynamical systems are easy to evaluate. We demonstrate the utility of dynamic teleportation on both the article graph of Wikipedia, where the external interest information is given by the number of hourly visitors to each page, and the Twitter social network, where external interest is the number of tweets per month. For these problems, we show that using information from the dynamical system helps improve a prediction task and identify trends in the data.
Ryan Rossi and David Gleich: Dynamic PageRank using Evolving Teleportation, Algorithms and Models for the Web Graph, volume 7323 of Lecture Notes in Computer Science, pages 126-137. Springer, 2012.
@article{rossi2012dynamic,
author = {Ryan A. Rossi and David F. Gleich},
title = {Dynamic {PageRank} using Evolving Teleportation},
booktitle = {Algorithms and Models for the Web Graph},
year = {2012},
editor = {Anthony Bonato and Jeannette Janssen},
volume = {7323},
series = {Lecture Notes in Computer Science},
pages = {126--137},
publisher = {Springer}
}
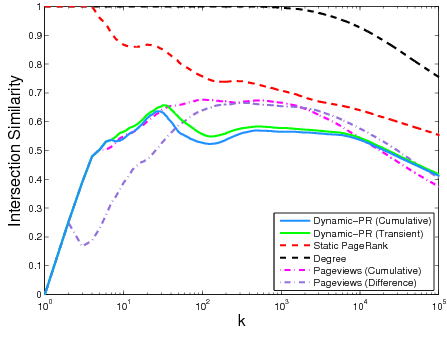
Other plots


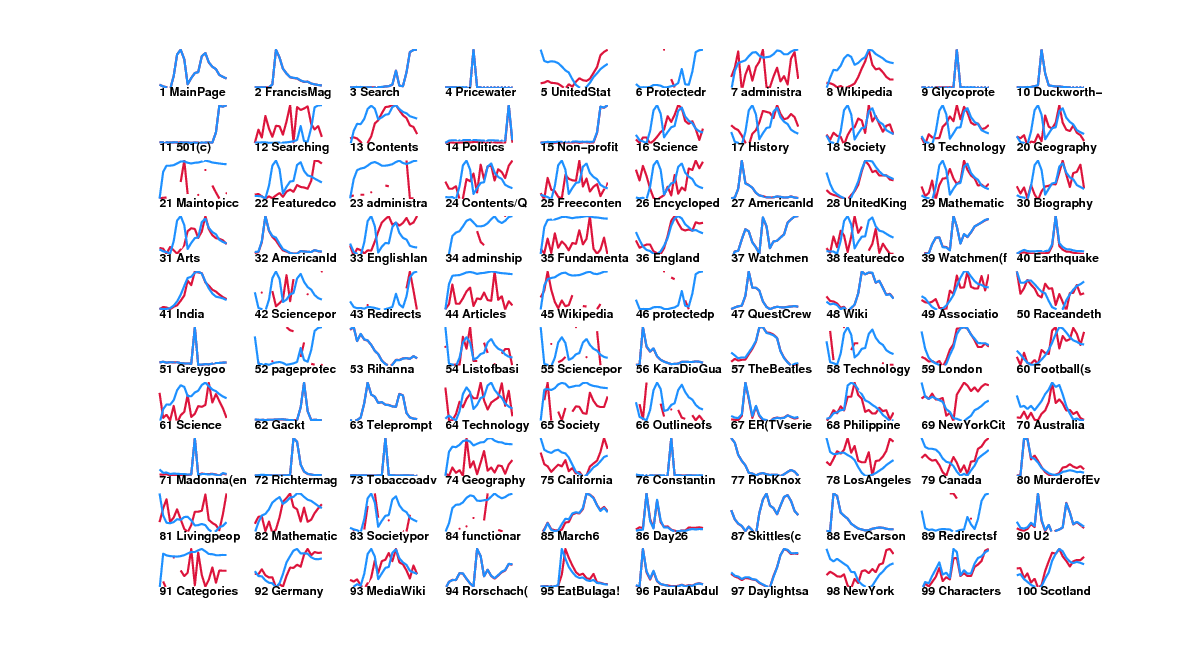
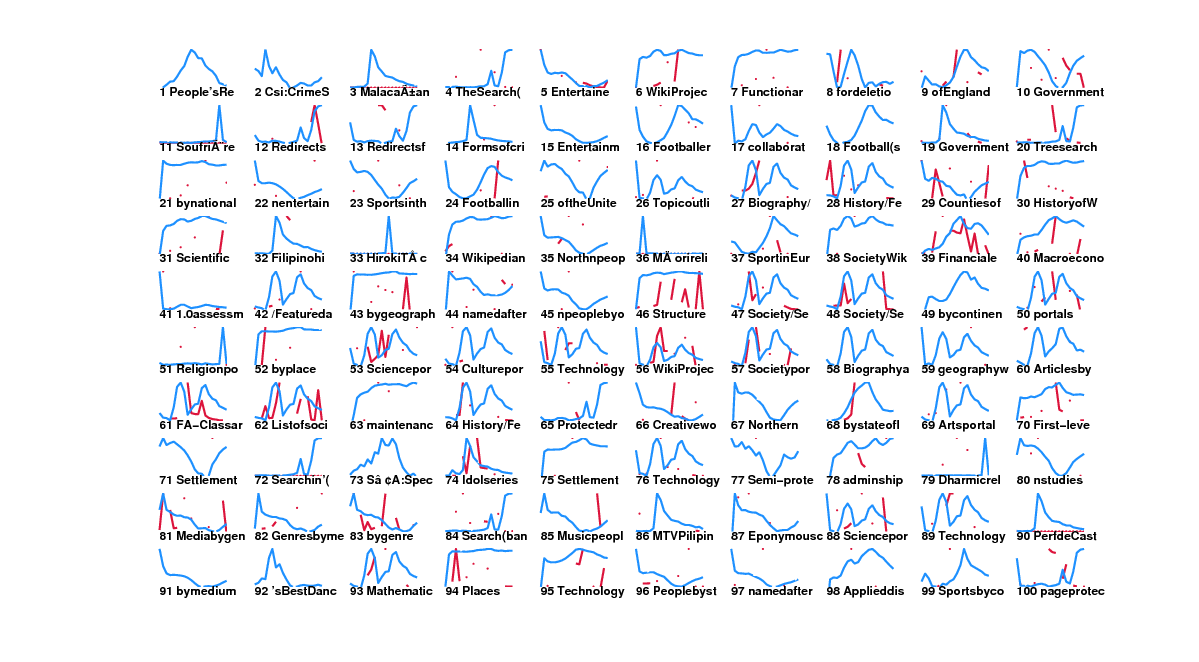
These are the top pages given by dynamic pagerank's difference ranking but not by pageviews difference ranking.
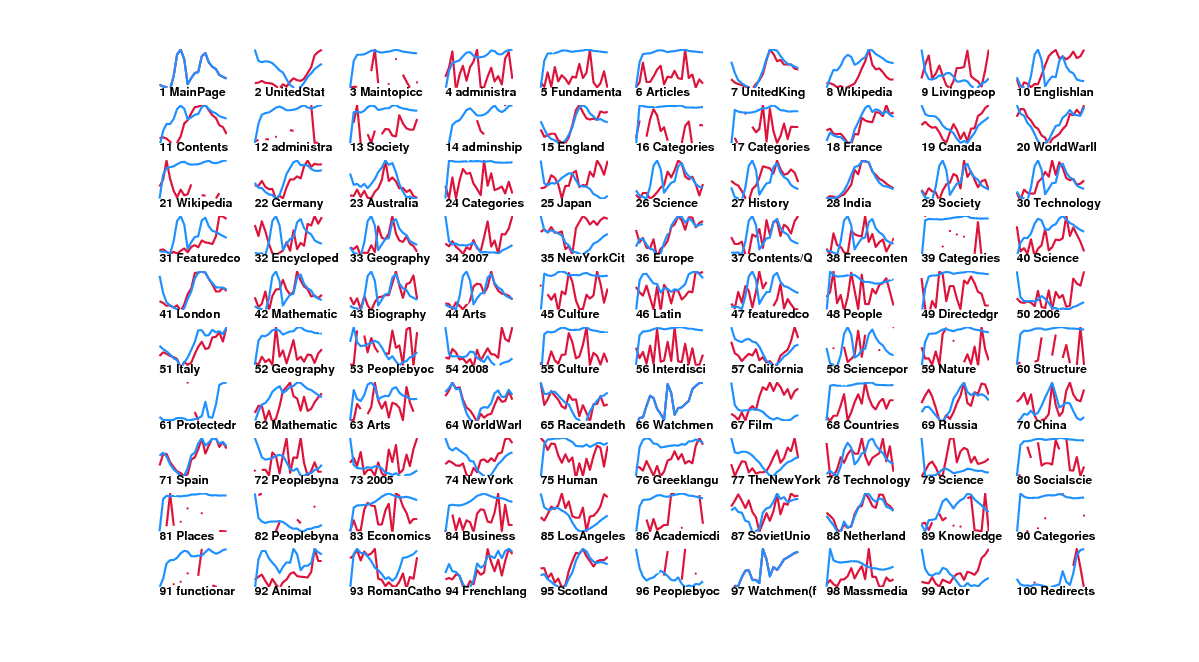
These are the top pages given by dynamic pagerank's cumulative ranking.
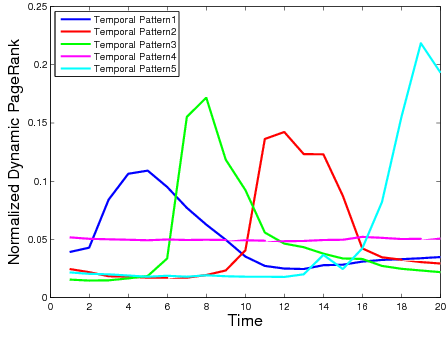
Clustering the Time-Series